9.2. Euclidean Topology¶
Let \(\mathbb{R}\) denote the set of all real numbers.
Definition
A subset \(S\) of \(\mathbb{R}\) is said to be open in the euclidean topology on \(\mathbb{R}\) if it has the following property:
(*) For each \(x \in S \quad \exists a,b \in \mathbb{R} \text{ and } a < b| x \in (a,b) \subseteq S\).
When we refer to topological space \(\mathbb{R}\) without specifying the topology, we mean \(\mathbb{R}\) with euclidean topology.
Every open interval \((a,b)\) is an open set.
The open intervals \((r,\infty)\) and \((-\infty, r)\) are open sets \(\forall r \in \mathbb{R}\).
While every open interval is an open set, not all open sets are intervals.
For each \(c,d \in \mathbb{R}\), the closed interval \([c,d]\) is not an open set.
For each \(a,b \in \mathbb{R}\), the closed interval \([a,b]\) is a closed set.
Each singleton set \(\{a\}\) is closed in \(\mathbb{R}\). Thus \(\mathbb{R}\) is a \(T_1\)-space.
The set \(\mathbb{Z}\) of all integers is a closed subset of \(\mathbb{R}\).
The set \(\mathbb{Q}\) of all rational numbers is neither a closed subset nor an open subset of \(\mathbb{R}\).
Definition
Let \((X,\mathcal{T})\) be a topological space. A subset \(S\) of \(X\) is said to be an \(F_{\sigma}\) -set if it is the union of a countable number of closed sets.
All open intervals \((a,b)\) and all closed intervals \([a,b]\) are \(F_\sigma\) -sets in \(\mathbb{R}\).
Definition
Let \((X,\mathcal{T})\) be a topological space. A subset \(T\) of \(X\) is said to be an \(G_{\sigma}\) -set if it is the intersection of a countable number of open sets.
All open intervals \((a,b)\) and all closed intervals \([a,b]\) are \(G_\sigma\) -sets in \(\mathbb{R}\).
\(\mathbb{Q}\) is an \(F_{\sigma}\) set in \(\mathbb{R}\) but not a \(G_{\sigma}\) set.
9.2.1. Basis¶
Proposition
A subset \(S\) of \(\mathbb{R}\) is open if and only if it is union of open intervals.
Definition
Let \((X, \mathcal{T})\) be a topological space. A collection \(\mathcal{B}\) of open subsets of \(X\) is said to be a basis for the topology \(\mathcal{T}\) if every open set is a union of the members of \(\mathcal{B}\).
\(\mathcal{B}\) generates the topology \(\mathcal{T}\) in the following sense: if we are told what sets are members of \(\mathcal{B}\), then we can determine the members of \(\mathcal{T}\).
Example
Let \(\mathcal{B} = \{(a,b) | a,b \in \mathbb{R}, a < b\}\). Then \(\mathcal{B}\) is a basis for the euclidean topology on \(\mathbb{R}\).
Remark
If \((X, \mathcal{T})\) is a topological space, then \(\mathcal{B} = \mathcal{T}\) is a basis for the topology \(\mathcal{T}\).
There can be many different bases for the same topology.
If \(\mathcal{B}\) is a basis for a topology \(\mathcal{T}\) on a set \(X\) and \(\mathcal{B}_1\) is a collection of subsets of \(X\) such that \(\mathcal{B} \subseteq \mathcal{B}_1 \subseteq \mathcal{T}\), then \(\mathcal{B}_1\) is also a basis for \(\mathcal{T}\).
Not any arbitrary collection of subsets of \(X\) can generate a topology.
Proposition
Let \(X\) be a non-empty set and let \(\mathcal{B}\) be a collection of subsets of \(X\). Then \(\mathcal{B}\) is a basis for a topology on \(X\) if and only if \(\mathcal{B}\) has the following properties.
\(X = \underset{B \in \mathcal{B}}{\cup} B\), and
for any \(B_1, B_2 \in \mathcal{B}\), the set \(B_1 \cap B_2\) is a union of members of \(\mathcal{B}\).
It is often easier to describing a topology by writing down its basis rather than describe all its open sets.
Example
Let \(\mathcal{B}\) be the collection of all “open rectangles” \(\{\langle x,y\rangle: \langle x,y\rangle \in \mathbb{R}^2, a < x < b, c < y < d\}\) in the plane which have each side parallel to the X- or Y-axis.
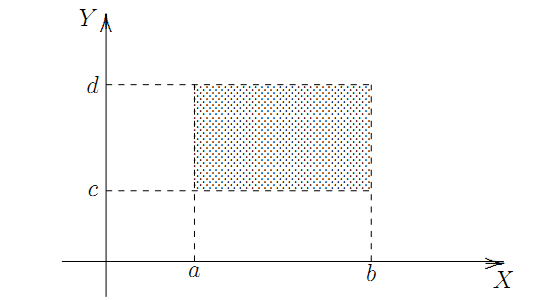
Then \(\mathcal{B}\) is a basis for a topology on the plane.
This topology is the euclidean topology of \(\mathbb{R}^2\).
\(\mathbb{R}^2\) means the plane, and if we refer to \(\mathbb{R}^2\) as a topological space without explicitly specifying the topology, we mean euclidean topology.
Remark
Let \(\mathbb{R}^n = \{\langle x_1, x_2, \dots, x_n \rangle : x_i \in \mathbb{R}, i = 1, \dots n \}\). Let \(\mathcal{B}\) be the collection of all subsets \(\{\langle x_1, x_2, \dots, x_n\rangle \in \mathbb{R}^n: a_i < x_i < b_i, i = 1,2,\dots, n\}\) with sides parallel to the axes. This collection \(\mathcal{B}\) is a basis for the euclidean topology on \(\mathbb{R}^n\).
Remark
Let \(\mathcal{B}_1\) be a basis for a topology \(\mathcal{T}_1\) on a set \(X\) and \(\mathcal{B}_2\) be a basis for a topology \(\mathcal{T}_2\) on a set \(Y\). The set \(X\times Y\) consists of all ordered pairs \(\langle x, y \rangle, x \in X, y \in Y\). Let \(\mathcal{B}\) be the collection of subsets of \(X\times Y\) consisting of all the sets \(B_1 \times B_2: B_1 \in \mathcal{B}_1, B_2 \in \mathcal{B}_2\). Then \(\mathcal{B}\) is a basis for a topology on \(X \times Y\). The topology so defined is called the product topology on \(X\times Y\).
9.2.2. Basis for a Given Topology¶
Sometimes we are given a topology \(\mathcal{T}\) on \(X\) and we want to verify whether \(\mathcal{B}\) is a basis for this specific topology \(\mathcal{T}\).
Proposition
Let \((X,\mathcal{T})\) be a topological space. A family \(\mathcal{B}\) of open subsets of \(X\) is a basis for \(\mathcal{T}\) if and only if for any point \(x \in U \text{ where } U \in \mathcal{T}\), there is a \(B \in \mathcal{B}\) such that \(x \in B \subseteq U\).
Proposition
Let \(\mathcal{B}\) be a basis for a topology \(\mathcal{T}\) on a set \(X\). Then a subset \(U \subseteq X\) is open if and only if for each \(x \in U \exists B \in \mathcal{B} | x \in B \subseteq U\).
How do we check whether two bases define the same topology?
Proposition
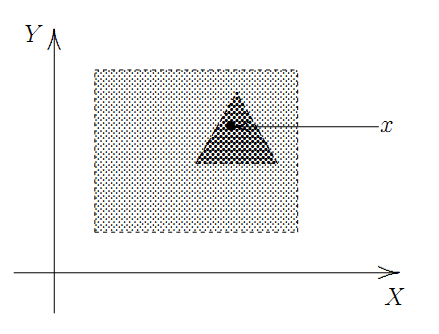
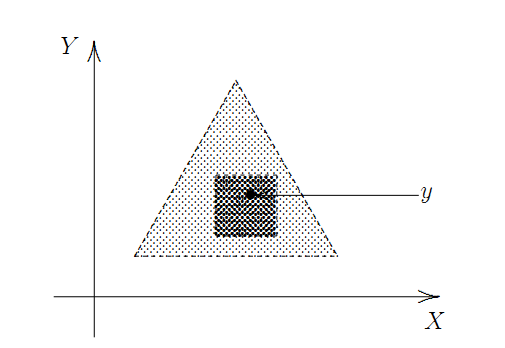
Let \(\mathcal{B}_1\) and \(\mathcal{B}_2\) be bases for topologies \(\mathcal{T}_1\) and \(\mathcal{T}_2\), respectively, on a non-empty set \(X\). Then \(\mathcal{T}_1=\mathcal{T}_2\) if and only if
for each \(B \in \mathcal{B}_1\) and each \(x \in B\), there exists a \(B' \in \mathcal{B}_2\) such that \(x \in B' \subseteq B\), and
for each \(B \in \mathcal{B}_2\) and each \(x \in B\), there exists a \(B' \in \mathcal{B}_1\) such that \(x \in B' \subseteq B\).
Example
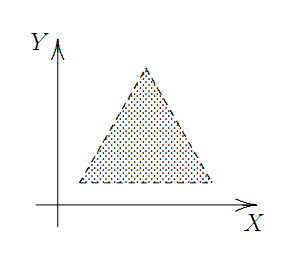
The set of all “open equilateral triangles” with base parallel to the X-axis is a basis for the euclidean topology on \(\mathbb{R}^2\).
The set of all open disks forms a basis for the euclidean topology on \(\mathbb{R}^2\).