9.6. Metric Spaces¶

Most important class of topological spaces
Provide a rich source of examples
Most applications of topology to analysis are via metric spaces

9.6.1. Metric Spaces¶

Definition

Let $X$ be a non-empty set and $d$ a real-valued function defined on $X \times X$ such that for $a,b \in X$:

$d(a,b) \geq 0$ and $d(a,b) = 0 \iff a = b$;
$d(a,b) = d(b,a)$; and
$d(a,c) \leq d(a,b) + d(b,c)$, [the triangle inequality] $\forall a,b,c \in X$.

Then $d$ is said to be a metric on $X$, $(X,d)$ is called a metric space and $d(a,b)$ is referred to as the distance between $a$ and $b$.

Example

The function $d: \mathbb{R} \times \mathbb{R} \mapsto \mathbb{R}$ given by

\[d(a,b) = |a-b|, \quad a,b \in \mathbb{R}\]

is a metric on the set $\mathbb{R}$ known as the euclidean metric.
The function $d : \mathbb{R}^2 \times \mathbb{R}^2 \mapsto \mathbb{R}$ given by

\[d( \langle a_1, b_1 \rangle, \langle a_2,b_2 \rangle ) = \sqrt{ (a_1 - b_1)^2 + (a_2 - b_2)^2}\]

is a metric on $\mathbb{R}^2$.
Let $X$ be a non-empty set and $d$ the function from $X\times X$ into $\mathbb{R}$ defined by

\[\begin{split}d(a,b) = \left\{ \begin{array}{ll} 0 & \mbox{if $a = b$}\\ 1 & \mbox{if $a \neq b$} \end{array} \right.\end{split}\]

Then $d$ is a metric on $X$ and is called the discrete metric.

9.6.1.1. Function Spaces¶

Let $C[0,1]$ denote the set of continuous functions from $[0,1]$ into $\mathbb{R}$. A metric is defined on this set by

\[d(f,g) = \int_0^1 |f(x) - g(x)| dx\]

where $f,g$ are in $C[0,1]$.

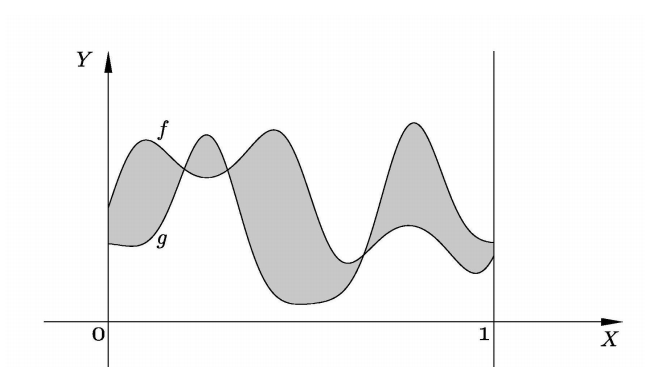
$d(f,g)$ is precisely the area of the region which lies between the graphs of functions.
Now, Another metric is defined on $C[0,1]$ as follows:

\[d^*(f,g) = \text{sup}\{|f(x) - g(x)| : x \in [0,1] \}\]

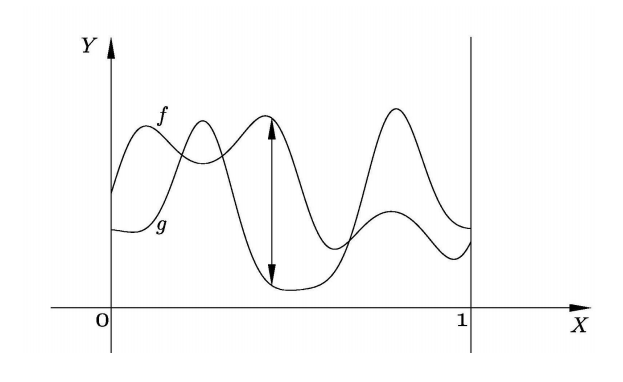
Clearly $d^*(f,g)$ is just the largest vertical gap between the graphs of functions $f$ and $g$.
More metrics on $\mathbb{R}^2$:

\[\begin{split}&d( \langle a_1, b_1 \rangle, \langle a_2,b_2 \rangle ) = \max\{ |a_1 - b_1 | , | a_2 - b_2 | \}\\ &d( \langle a_1, b_1 \rangle, \langle a_2,b_2 \rangle ) = |a_1 - b_1 | + | a_2 - b_2 |\end{split}\]

9.6.1.2. Normed vector spaces¶

Let $V$ be a vector space over the field of real or complex numbers. A norm $\parallel \text{ } \parallel$ on $V$ is a map $V \mapsto \mathbb{R}$ such that for all $a,b \in V$ and $\alpha$ in the field:

$\parallel a \parallel \geq 0$ and $\parallel a \parallel = 0 \iff a = 0$,
$\parallel a + b \parallel \leq \parallel a \parallel + \parallel b \parallel$, and
$\parallel \alpha a \parallel = |\alpha | \parallel a \parallel$.

A normed vector space is a vector space with a norm.

Let $(V, \parallel \parallel)$ be any normed vector space. Then there is a corresponding metric, $d$, on the set $V$ given by $d(a,b) = \parallel a - b \parallel \quad \forall a,b \in V$.

9.6.2. Metric Spaces as Topological Spaces¶

Open balls

In a normed vector space, the open ball with center a and radius r is defined to be the set

\[B_r(a) = \{x : x \in V | \parallel x - a \parallel < r\}\]

Why not generalize?

Definition

Let $(X,d)$ be a metric space and $r$ any positive real number. Then the open ball about $a \in X$ of radius $r$ is the set

\[B_r(a) = \{x : x \in X | d(a,x) < r\}\]

Example

The shape of the open ball depends on the choice of metric.

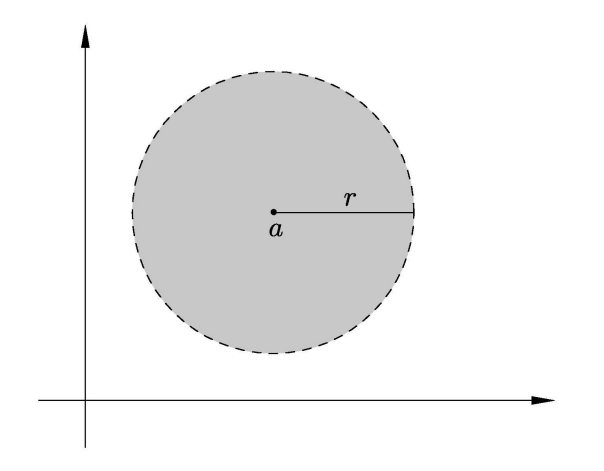
$\mathbb{R}^2$ with euclidean metric

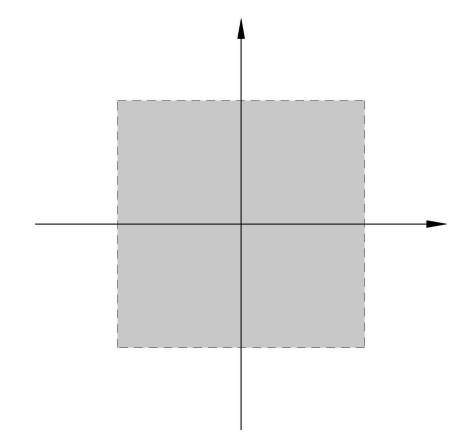
$d^*( \langle a_1, b_1 \rangle, \langle a_2,b_2 \rangle ) = \max\{ |a_1 - b_1 | , | a_2 - b_2 | \}$

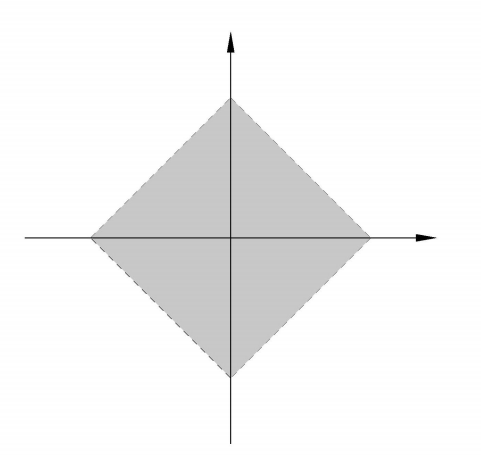
$d_1( \langle a_1, b_1 \rangle, \langle a_2,b_2 \rangle ) = |a_1 - b_1 | + | a_2 - b_2 |$

What happens in the intersection of open balls?

Lemma

Let $(X,d)$ be a metric space and $a$ and $b$ points of $X$. Further let $\delta_1$ and $\delta_2$ be positive real numbers. If $c \in B_{\delta_1}(a) \cap B_{\delta_2}(b)$, then there exists a $\delta > 0$ such that $B_{\delta}(c) \subseteq B_{\delta_1}(a) \cap B_{\delta_2}(b)$

Do open balls look like open sets?

Corollary

Let $(X,d)$ be a metric space and $B_1$ and $B_2$ open balls in $(X, d)$. then $B_1 \cap B_2$ is union of open balls in $(X,d)$.

So we do have a basis!

Proposition

Let $(X,d)$ be a metric space. Then the collection of open balls in $(X,d)$ is a basis for a topology $\mathcal{T}$ on $X$.

$\mathcal{T}$ is referred to as the topology induced by metric d.

$(X, \mathcal{T})$ is called the induced topological space or the corresponding topological space or the associated topological space.

Example

If $d$ is the discrete metric on a set $X$, then for each $x \in X, B_{\frac{1}{2}}(x) = \{x\}$. So all singleton sets are open in topology $\mathcal{T}$ induced on $X$ by $d$. Thus $\mathcal{T}$ is the discrete topology.
The euclidean metric on $\mathbb{R}$ induces the euclidean topology on $\mathbb{R}$. Ditto for $\mathbb{R}^2$.
But the other metrics $d^*$ and $d_1$ also induce euclidean topology on $\mathbb{R}^2$.

Different metrics can induce same topology!

Definition

Metrics on a set $X$ are said to be equivalent if they induce the same topology on $X$.

So whats the relation between open balls and open sets?

Proposition

Let $(X, d)$ be a metric space and $\mathcal{T}$ the topology induced on $X$ by the metric $d$. Then a subset $U$ of $X$ is open in $(X, \mathcal{T})$ if and only if for each $x \in U$ there exists an $\epsilon > 0$ such that the open ball $B_{\epsilon}(a) \subseteq U$

Is every topology induced by a metric?

9.6.2.1. Metrizable Spaces¶

Definition

A topological space $(X, \mathcal{T})$ is said to be a Hausdorff space or a $T_2$-space if for each pair of distinct points $a$ and $b$ in $X$, there exist open sets $U$ and $V$ such that $a\in U, b\in V$, and $U\cap V = \phi$.

Proposition

Let $(X, d)$ be any metric space and $\mathcal{T}$ the topology induced on $X$ by $d$. Then $(X, \mathcal{T})$ is a Hausdorff space.

Any set with 2 or more elements which has the indiscrete topology is not a Hausdorff space.
$\mathbb{Z}$ with finite closed topology is not a Hausdorff space.

Definition

A space $(X, \mathcal{T})$ is said to be metrizable if there exists a metric $d$ on the set $X$ with the property that $\mathcal{T}$ is the topology induced by $d$.

Warning

Every Hausdorff space is not metrizable. Though every metrizable space is a Hausdorff space.

Every subspace of a metrizable space is metrizable.

9.6.2.2. Bounded Metrics¶

Definition

A metric space $(X, d)$ is said to be bounded, and $d$ is said to be a bounded metric if there exists a positive real number $M$ such that $d(x,y) < M$, for all $x,y \in X$.

Every metric is equivalent to a bounded metric.

9.6.2.3. l_p spaces¶

Let $l_1$ be the set of all sequences of real numbers

\[x = (x_1,x_2, \dots, x_n, \dots)\]

with the property that the series $\sum_{n=1}^{\infty}|x_n|$ is convergent. If we define

\[d_1(x,y) = \sum_{n=1}^{\infty}|x_n - y_n| \quad \forall x, y \in l_1\]

Then $(l_1, d_1)$ is a metric space.
Let $l_2$ be the set of all sequences of real numbers

\[x = (x_1,x_2, \dots, x_n, \dots)\]

with the property that the series $\sum_{n=1}^{\infty}x_n^2$ is convergent. If we define

\[d_2(x,y) = (\sum_{n=1}^{\infty}|x_n - y_n|^2)^{\frac{1}{2}} \quad \forall x, y \in l_2\]

Then $(l_2, d_2)$ is a metric space.
Let $l_{\infty}$ be the set of bounded sequences of real numbers $x = (x_1,x_2, \dots, x_n, \dots)$. If we define

\[d_{\infty}(x,y) = \sup\{|x_n - y_n| : n \in \mathbb{N} \} \quad \forall x, y \in l_{\infty}\]

Then $(l_{\infty}, d_{\infty})$ is a metric space.
Each of the above spaces is a normed vector space in a natural way.

9.6.2.4. Normal Space¶

Definition

A topological space $(X, \mathcal{T})$ is said to be a normal space if for each pair of disjoint closed sets $A$ and $B$, there exist open sets $U$ and $V$ such that $A\subseteq U, B \subseteq V$ and $U\cap V = \phi$.

Every metrizable space is a normal space.

Definition

Let $(X,d_1)$ and $(Y, d_2)$ be metric spaces. Then $(X,d_1)$ is said to be isometric to $(Y,d_2)$ if there exists a surjective mapping $f : (X,d_1) \mapsto (Y,d_2)$ such that for all $x_1, x_2 \in X$

\[d_1(x_1, x_2) = d_2(f(x_1), f(x_2))\]

Such a mapping is called isometry.

Every isometry is a homeomorphism of the corresponding topological spaces.

9.6.2.5. Locally Euclidean¶

Definition

A topological space $(X, \mathcal{T})$ is said to be locally euclidean if there exists a positive integer $n$ such that each point $x \in X$ has an open neighborhood homeomorphic to an open ball about $0 \in \mathbb{R}^n$ with the euclidean metric.

Every non-trivial interval $(a,b) \in \mathbb{R}$ is locally euclidean.
The unit circle in complex plane is locally euclidean.
Every topological space homeomorphic to $\mathbb{R}^n$ is locally euclidean.

9.6.2.6. Manifold¶

Definition

A Hausdorff locally euclidean space is said to be a topological manifold.

There are many different kinds of manifolds (when more structure is imposed).

Differentiable manifolds
Smooth manifolds
Riemannian manifolds
Cauchy-Riemannian manifolds (CR-manifolds)

9.6.3. Convergence of Sequences¶

Definition

Let $(X,d)$ be a metric space and $x_1, \dots, x_n, \dots$ a sequence of points in $X$. Then the sequence is said to converge to $x \in X$ if given any $\epsilon > 0$, there exists an integer $n_0$ such that for all $n > n_0, d(x,x_n) < \epsilon$. This is denoted by $x_n \to x$.

The sequence $y_1, y_2, \dots, y_n, \dots$ of points in $(X, \mathcal{T})$ is said to be convergent if there exists a point $y \in X$ such that $y_n \to y$.

Convergence is unique!

Proposition

Let $x_1, x_2, \dots, x_n, \dots$ be a sequence of points in a metric space $(X, d)$. Further, let $x$ and $y$ be points in $(X,d)$ such that $x_n \to x$ and $x_n \to y$. Then $x = y$.

Convergence describes topology!

Proposition

Let $(X,d)$ be a metric space. A subset $A$ of $X$ is closed in $(X,d)$ if and only if every convergent sequence of points in $A$ converges to a point in $A$.

(In other words, $A$ is closed in $(X,d)$ if and only if $a_n \to x$, where $x \in X$ and $a_n \in A$ for all $n$, implies $x \in A$.)

Naturally convergence also describes continuous functions!

Proposition

Let $(X,d)$ and $(Y,d_1)$ be metric spaces and $f$ a mapping of $X$ into $Y$. Let $\mathbf{\tau}$ and $\mathbf{\tau}_1$ be the topologies determined by $d$ and $d_1$, respectively. Then $f : (X, \mathbf{\tau})\mapsto (Y, \mathbf{\tau}_1)$ is continuous if and only if $x_n \to x \implies f(x_n) \to f(x);$ i.e., if $x_1, x_2,\dots, x_n, \dots$ is a sequence of points in $(X,d)$ converging to $x$, then the sequence of points $f(x_1), f(x_2),\dots, f(x_n), \dots$ in $(Y, d_1)$ converges to $f(x)$.

Corollary

$f : (X, \mathbf{\tau})\mapsto (Y, \mathbf{\tau}_1)$ (as above) is continuous if and only if for each $x_0 \in X$ and $\epsilon > 0$, there exists a $\delta > 0$ such that $x \in X$ and $d(x,x_0) < \delta \implies d_1(f(x), f(x_0)) < \epsilon$.

distance between sets

Definition

Let A and B be non-empty sets in a metric space $(X,d)$. Define

\[\rho(A,B) = \inf\{d(a,b) : a \in A, b \in B\}\]

Then $\rho(A,B)$ is referred to as the distance between sets A and B.

9.6.4. Completeness¶

Definition

A sequence $x_1, x_2, \dots, x_n, \dots$ of points in a metric space $(X,d)$ is said to be a Cauchy sequence if given any real number $\epsilon > 0$, there exists a positive number $n_0$, such that for all integers $m > n_0, n > n_0$, we have $d(x_m, x_n) < \epsilon$.

Every convergent sequence is a Cauchy sequence.

Proposition

Let $(X,d)$ be a metric space and $x_1, x_2, \dots, x_n \dots$ a sequence of points in $(X,d)$. If there exists a point $a \in X$, such that the sequence converges to $a$, i.e. $x_n \to a$, then the sequence is a Cauchy sequence.

But every Cauchy sequence need not be convergent.

Example

Consider the open interval $(0,1)$ with the euclidean metric $d$.
It is clear that the sequence $0.1, 0.01, 0.001, 0.0001, \dots$ is a Cauchy sequence but it does not converge to any point in $(0,1)$.

Definition

A metric space is called to be complete if every Cauchy sequence in $(X,d)$ converges to a point in $(X,d)$.

Thus we see that $(0,1)$ with the euclidean metric is not a complete metric space.
If $X$ is any finite set and $d$ is the discrete metric on $X$, then $(X,d)$ is a complete metric space.
$\mathbb{R}$ with the euclidean metric is a complete metric space. How?
We will denote $x_1, x_2, \dots, x_n \dots$ by $\{x_n\}$.

Definition

If $\{x_n\}$ is any sequence, then the sequence $\{x_{n_1}, x_{n_2}, \dots\}$ is said to be a subsequence if $n_1 < n_2 < n_3 < \dots$.

Definitions

Let $\{x_n\}$ be a sequence in $\mathbb{R}$. Then it is said to be an increasing sequence if $x_n \leq x_{n+1} \quad\forall n \in \mathbb{N}$.

It is said to be a decreasing sequence if $x_n \geq x_{n+1} \quad\forall n \in \mathbb{N}$.

A sequence which is either increasing or decreasing is said to be a monotonic sequence.

Most sequences off course are neither increasing nor decreasing.

Definition

Let $\{x_n\}$ be a sequence in $\mathbb{R}$. Then $n_0 \in \mathbb{N}$ is said to be a peak point if $x_n \leq x_{n_0} \quad \forall n \geq n_0$.

Lemma

Let $\{x_n\}$ be a sequence in $\mathbb{R}$. Then $\{x_n\}$ has a monotonic subsequence.

If $\{x_n\}$ has infinite number of peak points, then the subsequence of peak points is a decreasing subsequence.
Otherwise there exists an integer $N$ such that there are no peak points for $n > N$. Choose any $n_1 > N$. We can find $n_2 > n_1 | x_{n_2} > x_{n_1}$ since $n_1$ is not a peak point. Similarly we can find $n_3 > n_2$. This way we can find an increasing sequence (by mathematical induction).

Proposition

Let $\{x_n\}$ be a monotonic sequence in $\mathbb{R}$ with the euclidean metric. Then $\{x_n\}$ converges to a point in $\mathbb{R}$ if and only if $\{x_n\}$ is bounded.

If $\{x_n\}$ is unbounded, then naturally it doesn’t converge.
Assuming $\{x_n\}$ as an increasing bounded sequence, there is a least upper bound $L$ of the the set $\{x_n\}, n \in \mathbb{N}$.
Thus $\forall \epsilon > 0, \exists N > 0 | d(x_N, L) < \epsilon$
Since $\{x_n\}$ is increasing, hence we have

\[L - \epsilon < x_n < L \quad \forall n > N.\]

(Bolzano-Weierstrass Theorem)

Every bounded sequence in $\mathbb{R}$ with euclidean metric has a convergent subsequence.

Corollary

The metric space $\mathbb{R}$ with the euclidean metric is a complete metric space.

We have to show that every Cauchy sequence converges in $\mathbb{R}$.
$\exists N > 0 | \forall m, n \geq N, d(x_n, x_m) < 1$.
$M = |x_1| + |x_2| + \dots + |x_N| + 1$ is an upper bound. Hence $\{x_n\}$ is bounded, hence has a convergent subsequence $\{x_{n_k}\}$ with $x_{n_k} \to a$.
Choose $\epsilon > 0$. Then $\exists N_0 > 0$ such that

\[|x_n - x_m| < \frac{\epsilon}{2}\quad \forall m,n \geq N_0.\]
Also $\exists N_1 > 0$ such that

\[|x_{n_k} - a| < \frac{\epsilon}{2}\quad \forall n_k \geq N_1.\]
Choose $N = \max(N_0, N_1)$. Then

\[|x_n - a| < \epsilon\quad \forall n \geq N.\]

Corollary

For each positive integer $m$, the metric space $\mathbb{R}^m$ with the euclidean metric is a complete metric space.

A normed vector space which is complete is called a Banach space.
An inner product space which is complete is called a Hilbert space.
The space $C[a,b]$ of continuous real valued functions on a closed and bounded interval is a Banach space, and so is a complete metric space w.r.t. the supremum norm.

9.6.4.1. Completeness and subspaces¶

Proposition

Let $(X,d)$ be a metric space, $Y$ a subset of $X$, and $d_1$ the metric induced on $Y$ by $d$.

If $(X,d)$ is a complete metric space and $Y$ is a closed subspace of $(X,d)$, then $(Y,d_1)$ is a complete metric space.
If $(Y,d_1)$ is a complete metric space, then $Y$ is a closed subspace of $(X,d)$.

$(0,1)$ is not complete while $[0,1]$ is complete.
$(0,1)$ is homeomorphic to $\mathbb{R}$. But $\mathbb{R}$ is complete while $(0,1)$ is not. Hence completeness is not a topological property (preserved by homeomorphism).

Definition

A topological space $(X, \mathcal{T})$ is said to be completely metrizable if there exists a metric $d$ on $X$ such that $\mathcal{T}$ is the topology on $X$ determined by $d$ and $(X,d)$ is a complete metric space.

Being completely metrizable is a topological property.
The topological spaces $\mathbb{R}$, $[a,b], (a,b), [a,b), (a,b]$, $(-\infty, a), (-\infty, a], (a, \infty), [a, \infty)$ and $\{a\}$ are all completely metrizable.
The space $\mathbb{P}$ of irrational numbers with the induced topology is completely metrizable.

Definition

A topological space is said to be separable if it has a countable dense subset.

Definition

A topological space is called Polish space if it is separable and completely metrizable.

$\mathbb{R}$ is a polish space, so is $\mathbb{R}^n$.

Definition

A topological space $(X,\mathcal{T})$ is said to be a Souslin space if it is Hausdorff and a continuous image of a Polish space. If $A$ is a subset of a topological space $(Y, \mathcal{T}_1)$ such that with the induced topology, the space $(A, \mathcal{T}_2)$ is a Souslin space, then $A$ is said to be an analytical set in $(Y, \mathcal{T}_1)$.

Every Polish space is a Souslin space since its a continuous image of itself and is a Hausdorff space (being a metric space).
Every Souslin space need not be metrizable.
Even a metrizable Souslin space is not necessarily a Polish space.
Analytic subsets of Polish spaces are closed under countable unions and intersections.
If the complement of an analytic set is analytic then the set is Borel.
Analytic sets are always Lebesgue measurable.
Topology > Metric Spaces > Measure Theory > Probability Theory

9.6.4.2. Metric space equivalence¶

Two topological spaces are equivalent if they are homeomorphic.
When are two metric spaces equivalent (as metric spaces)?

Definition

Let $(X,d)$ and $(Y,d_1)$ be metric spaces. Then $(X,d)$ is said to be isometric to $(Y,d_1)$ if there exists a surjective mapping $f : X \mapsto Y$ such that $\forall x_1, x_2 \in X, d(x_1, x_2) = d_1(f(x_1), f(x_2))$. Such a mapping is said to be an isometry.

The associated topological spaces of two isometric spaces are homeomorphic.

Definition

Let $(X,d)$ and $(Y,d_1)$ be metric spaces and $f$ a mapping of $X$ into $Y$. Let $Z = f(X)$, and $d_2$ be the metric induced on $Z$ by $d_1$. If $f:(X,d) \mapsto (Z, d_1)$ is an isometry, then $f$ is said to be an isometric embedding of $(X,d)$ in $(Y,d_1)$.

Natural embedding of $\mathbb{Q}$ with euclidean metric in $\mathbb{R}$ with euclidean metric is an isometric embedding.

9.6.4.3. Completion¶

Definition

Let $(X,d)$ and $(Y,d_1)$ be metric spaces and $f$ a mapping of $X$ into $Y$. If $(Y,d_1)$ is a complete metric space, $f$ is an isometric embedding and $f(X)$ is a dense subset of $Y$ in the associated topological space, then $(Y,d_1)$ is said to be a completion of $(X,d)$.

$\mathbb{R}$ is a completion of $\mathbb{Q}$ and $\mathbb{P}$.
Does every metric space has a completion?
Is the completion of a metric space unique in some sense?

Proposition

Let $(X,d)$ be a metric space. Then $(X,d)$ has a completion.

Two Cauchy sequences $\{y_n\}$ and $\{z_n\}$ are equivalent if $d(x_n, y_n) \to 0$ in $\mathbb{R}$.
This is an equivalence relation.
Let $\widetilde{X}$ be the set of all equivalence classes of Cauchy sequences.
Let $\tilde{y}$ and $\tilde{z}$ be two points in $\widetilde{X}$.
Let $\{y_n\} \in \tilde{y}$ and $\{z_n\} \in \tilde{z}$.
The sequence $d(y_n, z_n)$ is a Cauchy sequence in $\mathbb{R}$; converges to say $d_1(\tilde{y}, \tilde{z})$.
For each $x \in X$, the sequence $x,x,x,\dots$ is a Cauchy sequence which converges to $x$.
Let $\tilde{x}$ denote the equivalence class of all Cauchy sequences converging to $x \in X$.
Define $Y = \{\tilde{x} | x \in X\}$ as $Y \subseteq \widetilde{X}$.
Let $d_2$ be metric induced on $Y$ by $d_1$.
$f : (X,d) \mapsto (Y, d_2)$ with $f(x) = \tilde{x}$ is an isometry.
We can show that $Y$ is dense in $\widetilde{X}$.
We can show that $(\widetilde{X}, d_1)$ is a complete metric space.

Can an isometry over a subset help find an isometry over the containing spaces?

Proposition

Let $(A, d_1)$ and $(B, d_2)$ be two complete metric spaces. Let $X$ be a subset of $(A, d_1)$ with induced metric $d_3$ and $Y$ be a subset of $(B, d_2)$ with induced metric $d_4$ . Further let $X$ be dense in $(A, d_1)$ and $Y$ dense in $(B, d_2)$.

If there is an isometry $f : (X,d_3) \mapsto (Y, d_4)$, then there exists an isometry $g : (A, d_1) \mapsto (B, d_2)$, such that $g(x) = f(x) \forall x \in X$.

Proof outline

For every $a \in A \quad \exists x_n \to a | x_n \in X$ and $f(x_n) \to b | b \in B$
Define $g(a) = b \forall a \in A$.
Show that $g$ so defined is a well defined map.
Show that $g$ is one-one and onto.
Show that $g$ preserves distances hence is an isometry.

Further

A metric space may have several completions but they are isometric to each other.
So completion of a metric space is unique subject to isometries

9.6.4.4. Banach spaces¶

Definition

Let $(N, \| \|)$ be a normed vector space and $d$ the associated metric on the set $N$. Then $(N, \| \|)$ is said to be a Banach space if $(N,d)$ is a complete metric space.

Every normed vector space has a completion.
This completion is also a normed vector space.
So this completion is a Banach space.

9.6.5. Contraction mappings¶

Quite specific to metric spaces rather than general topology.

Definition

Let $f : X \to X$ be a mapping of a set $X$ into itself. Then a point $x \in X$ is said to be a fixed point of $f$ if $f(x) = x$.

Definition

Let $(X,d)$ be a metric space and $f : X \to X$ a mapping of $X$ into itself. Then $f$ is said to be a contraction mapping if there exists an $r \in (0,1)$ such that $d(f(x_1), f(x_2)) \leq r\cdot d(x_1, x_2) \forall x_1,x_2 \in X$.

Proposition

Let $f$ be a contraction mapping over $(X,d)$. Then $f$ is a continuous mapping.

Theorem (Contraction mapping theorem or Banach fixed point theorem)

Let $(X,d)$ be a complete metric space and $f$ a contraction mapping on $(X,d)$ into itself. Then $f$ has precisely one fixed point.

Proof outline

We show that $x, f(x), f^2(x),\dots, f^n(x),\dots$ is a Cauchy sequence and $f^n(x) \to z \in X$.
We show that $f(z) = z$, hence is a fixed point.
We show that $z$ is unique.

9.6.6. Baire spaces¶

Theorem (Baire Category Theorem)

Let $(X,d)$ be a complete metric space. If $X_1, X_2,\dots, X_n,\dots$ is a sequence of open dense subsets of $X$, then the set $\cap_{i=1}^{\infty} X_i$ is also dense in $X$.

Definition

Let $(X, \mathcal{T})$ be any topological space and $A$ any subset of $X$. The largest open set contained in $A$ is said to be the interior of A and is denoted by $\text{int}(A)$

Definition

A subset $A$ of a topological space $(X,\mathcal{T})$ is said to be nowhere dense if the set $\overline{A}$ has empty interior.

Definition

The boundary of a set $A$ in $(X,\mathcal{T})$ is defined by $B = \overline{A} \cap \overline{X \setminus A}$

Boundary of a set is a closed set (its an intersection of two closed sets)
Boundary of an open ball $B_{r}(x) = \{ y \in X | d(y,x) < r\}$ is $\{y \in X | d(y,x) = r\}$.
Boundary of an open set $A$ can be given by $B = \overline{A} \cap {X \setminus A}$
Boundary of an open set is nowhere dense.
$\mathbb{Q}$ is not open and its boundary doesn’t have an empty interior.

Rephrasing the Baire Category Theorem

Corollary

Let $(X,d)$ be a complete metric space. If $X_1, X_2,\dots, X_n,\dots$ is a sequence of subsets of $X$, such that $X = \cup_{i=1}^{\infty}X_n$, then for at least one $n \in \mathbb{N}$, the set $\overline{X_n}$ has non empty interior, that is $X_n$ is not nowhere dense.

Definition

A topological space $(X,d)$ is said to be a Baire space if for every sequence $\{X_n\}$ of open dense subsets of $X$, the set $\cap_{i=1}^{\infty} X_i$ is also dense in $X$.

Corollary

Every completely metrizable space is a Baire space.

Above is a result in topology rather than a result in metric space theory.
There are Baire spaces which are not completely metrizable.
The topological space $\mathbb{Q}$ is not a Baire space and so is not completely metrizable.
It is easier to prove that $\mathbb{Q}$ is not a Baire space, than to prove that $\mathbb{Q}$ is not completely metrizable without this notion.

Definitions

Let $Y$ be a subset of a topological space $(X, \mathcal{T})$. If $Y$ is a union of a countable number of nowhere dense subsets of $X$, then $Y$ is said to be a set of the first category or meager in $(X,\mathcal{T})$. If $Y$ is not first category, it is said to be of second category in $(X,\mathcal{T})$.

Proposition

If $Y$ is a first category subset of a Baire space $(X, \mathcal{T})$ then the interior of $Y$ is empty.

Corollary

If $Y$ is a first category subset of a Baire space $(X,\mathcal{T})$, then $X \setminus Y$ is a second category set.

$\mathbb{Q}$ is a first category subset of $\mathbb{R}$.
$\mathbb{P}$ is a second category subset of $\mathbb{R}$.

Definition

Let $S$ be a subset of a real vector space $V$. The set $S$ is said to be convex if for each $x,y \in S$ and every real number $0 < \lambda < 1$, the point $\lambda x + (1 - \lambda) y \in S$.

Every subspace of a real vector space is convex.
Every open ball and every closed ball in a normed real vector space is convex.

Definition

Let $(X,\mathcal{T})$ and $(Y,\mathcal{T}_1)$ be topological spaces. A mapping $f: (X,\mathcal{T}) \to (Y,\mathcal{T}_1)$ is said to be an open mapping if for every open subset $A$ of $(X,\mathcal{T})$, the set $f(A)$ is open in $(Y,\mathcal{T}_1)$.

Theorem (Open Mapping Theorem)

Let $(B, \| \|)$ and $(B_1, \| \|_1)$ be Banach spaces and $L : B \to B_1$ a continuous linear (in the vector space sense) mapping of $B$ onto $B_1$. Then $L$ is an open mapping.

Corollary

A one to one continuous linear map of one Banach space onto another Banach space is a homeomorphism. In particular, a one to one continuous linear map of a Banach space onto itself is a homeomorphism.

9.6. Metric Spaces¶

9.6.1. Metric Spaces¶

9.6.1.1. Function Spaces¶

9.6.1.2. Normed vector spaces¶

9.6.2. Metric Spaces as Topological Spaces¶

9.6.2.1. Metrizable Spaces¶

9.6.2.2. Bounded Metrics¶

9.6.2.3. l_p spaces¶

9.6.2.4. Normal Space¶

9.6.2.5. Locally Euclidean¶

9.6.2.6. Manifold¶

9.6.3. Convergence of Sequences¶

9.6.4. Completeness¶

9.6.4.1. Completeness and subspaces¶

9.6.4.2. Metric space equivalence¶

9.6.4.3. Completion¶

9.6.4.4. Banach spaces¶

9.6.5. Contraction mappings¶

9.6.6. Baire spaces¶

Table of Contents

Previous topic

Next topic