9.4. Homeomorphisms¶
How do we identify that two topologies are equivalent?
9.4.1. Subspaces¶
Definition
Let \(Y\) be a non-empty subset of a topological space \((X, \mathcal{T})\). The collection \(\mathcal{T}_Y = \{O \cap Y : O \in \mathcal{T}\}\) of subsets of \(Y\) is a topology on \(Y\) called the subspace topology (or the relative topology or the induced topology). The topological space \((Y, \mathcal{T}_Y)\) is called to be a subspace of \((X,\mathcal{T})\).
Example
Let \(X = \{a, b, c, d, e, f\}\)
Let \(\mathcal{T} = \{X, \phi, \{a\}, \{c,d\}, \{a,c,d\}, \{b,c,d,e,f\} \}\)
And \(Y = \{b,c,e\}\)
Then the subspace topology on \(Y\) is:
\[\mathcal{T}_Y = \{Y, \phi, \{c\}\}\]
Remark
Let \(\mathcal{B}\) be a basis for the topology \(\mathcal{T}\) on \(X\). Let \(Y\) be a subset of \(X\). The the collection \(\mathcal{B}_Y = \{ B \cap Y : B \in \mathcal{B} \}\) is a basis for the subspace topology \(\mathcal{T}_Y\) on \(Y\).
Example
Consider the subset \((1,2)\) of \(\mathbb{R}\).
A basis for the induced topology on \((1,2)\) is the collection \(\{(a,b) \cap (1,2) : a,b\in \mathbb{R}, a < b \}\); that is \(\{ (a,b) : a, b \in \mathbb{R} , 1 \leq a < b \leq 2 \}\).
Example
Consider the subset \([1,2]\) of \(\mathbb{R}\).
A basis for the induced topology on \([1,2]\) is the collection \(\{(a,b) \cap [1,2] : a,b\in \mathbb{R}, a < b \}\); that is
\[\{(a,b): 1 \leq a < b \leq 2 \} \cup \{[1,b) : 1 < b \leq 2\} \cup \{ (a,2] : 1 \leq a < 2\} \cup \{ [1,2] \}\]As we can see: some sets which are not open in \(\mathbb{R}\) become open in the subspace topology.
Example
The topology induced on \(\mathbb{Z}\) by the euclidean topology on \(\mathbb{R}\) is the discrete topology.
Going forward whenever we refer to \((a,b), [a,b], [a,b), (-\infty, a), (-\infty, a], (a,\infty), [a, \infty)\) as topological spaces without explicitly stating the topology, we will mean the topology induced by the euclidean topology on \(\mathbb{R}\).
9.4.2. Homeomorphisms¶
Example
\(X = \{a,b,c,d,e\}\)
\(Y = \{g,h,i,j,k\}\)
\(\mathcal{T}_X = \{X,\phi, \{a\}, \{c,d\}, \{a,c,d\}, \{b,c,d,e\}\}\)
\(\mathcal{T}_Y = \{Y,\phi, \{g\}, \{i,j\}, \{g,i,j\}, \{h,i,j,k\}\}\)
Intuitively, the two topologies look equivalent. The function:
\[\begin{split}&f : X \rightarrow Y \\ &f(a) = g, f(b) = h, f(c) = i, f(d) = j, f(e) = k\end{split}\]provides the equivalence.
Definition
Let \((X, \mathcal{T}_1)\) and \((Y, \mathcal{T}_2)\) be topological spaces. Then they are said to be homeomorphic if there exists a function \(f : X \rightarrow Y\) which has the following properties:
\(f\) is one-one. \(f(x_1) = f(x_2) \implies x_1 = x_2\).
\(f\) is onto. \(\forall y \in Y \exists x \in X | f(x) = y\).
\(\forall U \in \mathcal{T}_2, \quad f^{-1} (U) \in \mathcal{T}_1\)
\(\forall V \in \mathcal{T}_1, \quad f(V) \in \mathcal{T}_2\)
Further the map \(f\) is said to be homeomorphism between \((X, \mathcal{T}_1)\) and \((Y, \mathcal{T}_2)\). We write \((X, \mathcal{T}_1) \cong (Y, \mathcal{T}_2)\).
Homeomorphism is a reflexive, symmetric, and transitive relation. Hence it is an equivalence relation.
Example
Every non empty open interval \((a,b)\) is homeomorphic to \((0,1)\).
\[f(x) = a(1-x) + bx\]
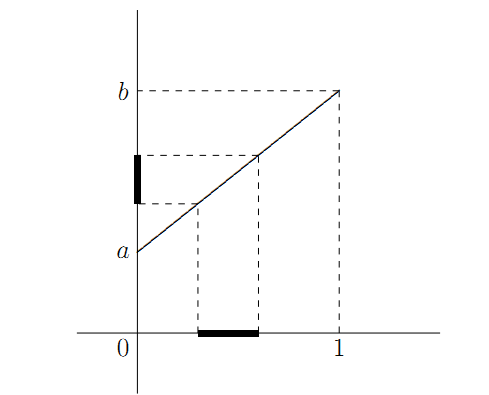
Every two non-empty open intervals \((a,b)\) and \((c,d)\) are homeomorphic.
\(\mathbb{R}\) is homeomorphic to \((-1,1)\).
\[f(x) = \frac{x}{1 - |x|}\]
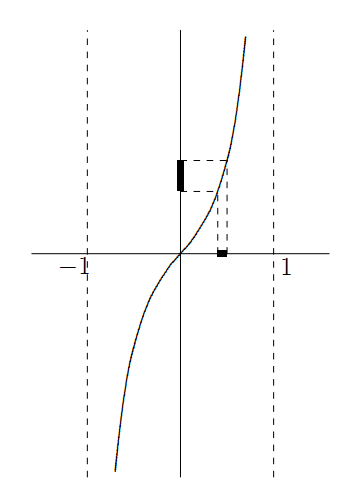
Thus every open interval \((a,b)\) is homeomorphic to \(\mathbb{R}\).
It shows that length is not a topological property.
Similarly any two closed intervals \([a,b]\) and \([c,d]\) are homeomorphic.
Let \(a, b \in \mathbb{R}\), then:
\[(-\infty,a] \cong (-\infty,b] \cong [a,\infty) \cong [b,\infty)\]
With \(c,d,e,f \in \mathbb{R}\) and \(c < d, e < f\), we have
\[[c,d) \cong [e,f) \cong (c,d] \cong (e,f]\]\(\mathbb{Z} \cong \mathbb{N}\)
Any line in \(\mathbb{R}^2\) given by \(X = \{\langle x, y \rangle : y = mx + c\}\) is homeomorphic to \(\mathbb{R}\).
Let \(X_1\) and \(X_2\) be the closed rectangular regions in \(\mathbb{R}^2\) given by
\[\begin{split}&X_1 = \{ \langle x,y \rangle : |x| \leq a_1 , |y| \leq b_1 \} \\ &X_2 = \{ \langle x,y \rangle : |x| \leq a_2 , |y| \leq b_2 \}\end{split}\]Then \(X_1 \cong X_2\) w.r.t. their induced topologies
Similarly any two closed discs in \(\mathbb{R}^2\) are homeomorphic.
Group of homeomorphisms
Let \((X,\mathcal{T})\) be any topological space and \(G\) the set of all homeomorphisms of \(X\) into itself. Then \(G\) is a group under the operation of composition of functions.
9.4.3. Non-Homeomorphic Spaces¶
Proving that two topological spaces are not homeomorphic is often much harder as we have to show that no homeomorphism exists.
Example
We show that \((X, \mathcal{T}_1) = [0,2]\) is not homeomorphic to the subspace \((Y, \mathcal{T}_2) = [0,1] \cup [2,3]\).
\([0,1]\) and \([2,3]\) are clopen sets in \((Y, \mathcal{T}_2)\)
Thus \((Y, \mathcal{T}_2)\) is not connected while \((X, \mathcal{T}_1)\) is connected.
If \(X \cong Y\), w.r.t. a homeomorphism \(f: (X, \mathcal{T}_1) \rightarrow (Y, \mathcal{T}_2)\) then there exists a clopen set \(f^{-1}([0,1]) \in X\), a contradiction.
Hence \(X \ncong Y\).
Proposition
Any topological space homeomorphic to a connected space is connected.
Properties preserved by homeomorphisms
Let \(X \cong Y\), w.r.t. a homeomorphism \(f: (X, \mathcal{T}_1) \rightarrow (Y, \mathcal{T}_2)\)
If one is a \(T_0\)-space, so is the other.
If one is a \(T_1\)-space, so is the other.
If one is a \(T_2\)-space or Hausdorff space, so is the other.
If one is a regular space, so is the other.
If one is a \(T_3\)-space, so is the other.
If one satisfies second axiom of countability, so does the other.
If one is a separable space, so is the other.
If one is connected, so is the other.
If one is a discrete space, so is the other.
If one is an indiscrete space, so is the other.
If one is a finite-closed topology, so is the other.
If one is a countable-closed topology, so is the other.
If one is countable so is the other.
If one is uncountable, so is the other.
If one is finite, so is the other with same cardinality.
We use above properties to verify if two topologies are homeomorphic or not.
Definition
A subset \(S\) of \(\mathbb{R}\) is said to be an interval if it has the following property: if \(x \in S, z \in S\), and \(y \in \mathbb{R}\) are such that \(x < y < z\), then \(y \in S\).
How is \((0,1) \ncong [0,1]\)?
Remark
Let \(f : (X, \mathcal{T}_1) \rightarrow (Y, \mathcal{T}_2)\) be a homeomorphism. Let \(a \in X\) so that \(X \setminus \{a\}\) be a subspace of \(X\) with an induced topology \(\mathcal{T}_3\). Also \(Y \setminus \{f(a)\}\) is a subspace of \(Y\) with an induced topology \(\mathcal{T}_4\). Then
Removing any element from an open interval makes it disconnected.
Removing the border element from a closed / semi-closed interval leaves it connected.
Corollary
If \(a,b,c,d\) are real numbers with \(a < b\) and \(c < d\), then
\((a,b) \ncong [c,d)\)
\((a,b) \ncong [c,d]\) and
\([a,b) \ncong [c,d]\)
Definition
A property is said to be topological if it is preserved by homeomorphisms.